【トピックス】
変数消去を切り口とした代数生物学の研究例の紹介
小松瑞果
神戸大院・システム
1.はじめに
従来、数理生物学分野において用いられる数理モデルの解析手法は、線形代数に基づくものが主流であった。しかし、代謝モデル、細胞間相互作用を表すモデル、薬物動態モデル、SIRモデル、ロトカボルテラモデルなど、実際に用いられているモデルの多くは非線形であり、これらに対し、必ずしも線形代数に基づく手法が有効とは限らない。このような背景のもと、生物学的現象を表す非線形モデルの多くが、特に、多項式微分方程式や代数方程式などを用いて記述されるという点に着目し、これらに対して有効な手法―代数的手法―を取り入れる研究が展開されている1-4)。また、より一般に、代数の概念・技術を生物学に関するモデリングに導入する研究が数多く存在し5,6)、これらを扱う学問分野は代数生物学などと呼ばれている7)。この分野は、2000年代中頃に始まり、今もなお成長し続けている分野である。
本稿では、代数生物学における研究例を紹介する。通常、代数生物学に関する文献の多くは、代数学における概念や知識などを列挙した後に、具体的な応用例を示す構成になっている。しかし、このような構成には、代数学における基礎概念や記号の用い方等を理解しなければ、その応用における価値を見出せないという難点がある。そこで、本稿は、生物学に関わる研究者が代数生物学に関心をもつきっかけとなることを狙いとし、モデリングの具体例を挙げつつ、連立代数方程式の求解という比較的親しみやすい話題を軸に説明を進める。また、代数に関する厳密な議論を避け、代数的手法が自然に必要となることやその有効性の説明に焦点を当てる。
連立方程式の求解における本質的な操作の一つは、変数消去である。連立代数方程式における変数消去は、代数学という広大な分野における一つの具体的な問題に過ぎないが、代数のエッセンスに触れられるトピックスでもある。そこで、本稿では生物学的現象を表す数理モデルに対する変数消去という切り口から、代数生物学の研究例を紹介する。具体的には、グレブナー基底を用いた変数消去の基礎と、生物学的現象のモデリングにおける問題-モデルリダクションやパラメータ推定など―への応用について述べる。4節の最後には、筆者らが構築した、観測データが限定的である場合に有効なパラメータ推定手法などにも触れる。
2. 多項式微分方程式や代数方程式が定めるモデルの具体例
生物学的現象を表す数理モデルの中には、多項式微分方程式や代数方程式によって記述されるモデルが数多く存在し、実際に用いられている。ここでは、これらの方程式を用いて記述されるよく知られた具体例として、酵素反応系のモデルを紹介する。
Sを基質、Eを酵素、Cを複合体、Pを生成物とする酵素反応系は、
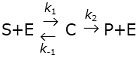
なる化学反応式で記述される。ここで、k1, k-1, k2は各素過程の反応速度定数を表す。これを質量作用の法則のもとモデル化すると
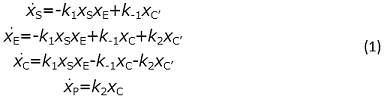
となる。ただし、xS, xE, xC, xPは、それぞれ、基質、酵素、複合体、生成物の濃度を表し、左辺は、これらの時間による微分を表す。以降、(1) と同様に、変数の時間微分をドット付きの変数により表記する。
(1) の右辺は、xS, xE, xC, xPを変数、k1, k-1, k2 (の関数) を係数とするような多項式である。このように、酵素反応系においては、質量作用の法則から自然に多項式表現が導かれる。本稿では、(1) のようなモデルを多項式微分方程式と呼ぶ。(1) について、複合体の定常状態を仮定すると、0 = k1xS xE-k-1 xC-k2 xCなる代数方程式が得られる。ここでは、定常状態の仮定から代数方程式が導かれている。酵素反応系に限らず、生物学的現象を表す数理モデルにおいては、現象の性質や仮定などから、多項式の表現や代数方程式が自然に導かれることが多い。
3.連立代数方程式における変数消去とグレブナー基底
一般に、多項式微分方程式や代数方程式を扱う際には、代数的手法が有効である。代数学における基本的な問題の一つとして、連立代数方程式の求解が挙げられ、ここで本質的となる手順の一つが変数消去である。変数消去は、実は生物学的現象のモデリングの諸問題に関連している。例えば、酵素反応系においては、準定常状態の仮定のもと、生成物等に関する方程式を導出し、これを解析することが多いが、これは変数消去に基づくモデルリダクションと捉えることができる8)。以下では、連立代数方程式における変数消去と、これを実現するため代数的な枠組みであるグレブナー基底について説明する。
以下では、3つの変数x, y, zに関する連立代数方程式
![]()
を例に用いる。通常、このような連立代数方程式を解く際、方程式に定数や変数をかけ、それらを足し引きするなどの式変形、すなわち、代数演算を通じた変数消去が行われる。例えば、x, yを消去するよう式変形を繰り返せば、2z4-3z2=-1が得られ、これを解くと、z=±1, ±1, / √2と求まる。さらに、これを別の式に代入すると、x, yの値もそれぞれ求まる。上記の手順で解が求まるものの、与えられた方程式が変わると、その手順も変わってしまう。そのため、一般の連立代数方程式を解くには、そのための枠組みが必要であり、このような場合にグレブナー基底が有効である。
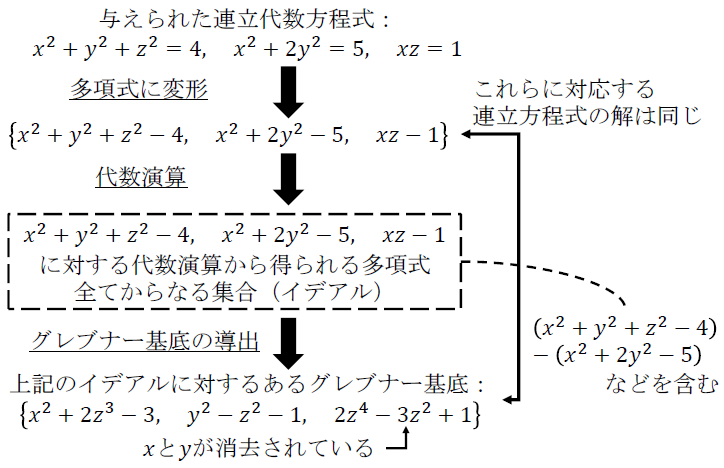
グレブナー基底に基づく枠組みでは、代数演算によって得られる個別の式を追うというより、そのような演算によって得られる多項式の集合全体を考える。具体的には、(x2+y2+z2-4)-(x2+2y2-5)や3(x2+y2+z2-4)+y(xz-1) などのような、(2) に対する代数演算によって導かれる多項式全てを含む集合に着目する。そして、この集合に対し、ある種の良い性質を満たす多項式集合 (基底) を導出する。少し専門的な表現を用いると、与えられた連立代数方程式に対する代数演算によって得られる多項式の集合全体をイデアルといい、グレブナー基底はこれを特徴づける多項式の集合である。連立代数方程式とこれに対応する多項式の集合、イデアル、及び、グレブナー基底の関係を図1に示す。

図1に記載の通り、グレブナー基底から求まる連立方程式の解は、所与の連立方程式の解に一致することが知られている。これは、グレブナー基底を用いると連立方程式の解が求められることを示唆している。
以下、グレブナー基底を用いた変数の消去、及び、連立代数方程式の求解の具体的な手順を概説する。グレブナー基底を導出するためのアルゴリズムとしてBuchbergerのアルゴリズム9)が知られており、その発展版や、効率の良い計算をするためのソフトウェアも多数開発されている10)。そのため、近年は、連立代数方程式を専用のソフトウェアに入力として与え、数行のプログラムを記述することで、比較的複雑な連立方程式の代数的な扱いが可能となりつつある。実際、(2) に対応するイデアルのグレブナー基底を、変数などの優先順位を指定したもとで計算すると
![]()
が得られる。ここで、第三式ではx及びyが消去されており、(第三式)=0から求まるzの値を(第一式)=0や(第二式)=0に代入すると、それぞれ、xとyの値が求まる。このような変数消去が行われているのは、変数消去が可能となるように変数などの優先順位を定めたことによる。このように、一定の条件下でグレブナー基底を計算することで、変数消去が実現され、これにより連立代数方程式の解を求めることができる。以上に述べたグレブナー基底に基づく代数的枠組みは、方程式によらず、一般の連立代数方程式に対して有効である。本稿では、グレブナー基底の定義や詳細な説明は避けたが、詳細については関心がある場合は、Coxらによる入門書9)などを参照されたい。
4.代数的手法の応用例-可同定性解析とその発展-
ここでは、数理生物分野のモデリングにおける変数消去の応用例として、多項式微分方程式の可同定性解析とその発展の位置づけにある研究例を紹介する。
ここで、(1) の第一式から第三式、及び、xEに関する時系列データが与えられたもとで、未知の反応速度定数k1,k-1, k2を推定するような、パラメータ推定問題を考える。これらのパラメータには反応速度に関連する生物学的意味が与えられており、これを推定することで現象 (酵素反応) の解釈を試みる、という設定である。
一般に、パラメータ推定を行う際のポイントの一つとして、パラメータがデータから一意に定まるかどうか、すなわち、モデルの可同定性をあらかじめ確認しておくことが挙げられる。実際、特定の意味が与えられたパラメータの値が一意に定まらないにも関わらず、何らかの手法によりこれを一意に推定し、その値のみからモデルや現象の考察を進めた場合、その他の可能性のある考察を見落とすことになる。(1) のモデルはあまり複雑でないため、そのような問題が生じない可能性があるが、観測データが限定的である場合や、モデルが複雑である場合11)に、このような問題が生じやすい。観測データにノイズが含まれていない、理想的な状況を仮定したもとで可同定性を解析することを、構造的可同定性解析と呼ぶ。構造的可同定性解析には、様々な手法があるが12)、特に、真のパラメータが含まれうる範囲が、事前知識などから絞りこめない場合には、代数的手法が有効である。
代数に基づく構造的可能同定性解析の手順は大きく二段階に分かれ、前半部分は、多項式微分方程式から、未観測変数を消去する問題に帰着される。ここで、モデルは微分方程式であるため、通常の連立代数方程式を解く場合と異なり、微分代数の概念を導入することとなる。微分代数とは、簡潔に述べると、微分を演算に含む代数である13)。(1) の場合には、左辺に時間による微分が現れており、今回は、このような時間による微分を演算として許容する。つまり、連立代数方程式の場合、代数演算を扱ったが、連立微分方程式の場合、これに微分演算が加わるということである。これらの二つの代数の理論には差異があるものの、適当に前処理を行ったもとで構造的可能同定性解析を行う際には、概ね同様の扱いが可能であることが示されている14)。実際、(1) とその微分に対応するイデアルのグレブナー基底を計算すると、未観測変数やその高階微分が現れない、観測された変数のみの微分方程式
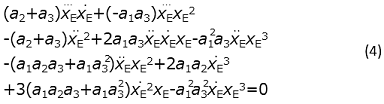
が得られる。観測変数xE及びその微 x…E, x¨E, x˙Eに関する複数時点の理想的なデータが与えられたとし、(4) の係数部分の値が一意に定まるか否かを解析することで、モデルの構造的可同定性が調べられる。具体的には、(4) に各時点のデータを与えた方程式を立て、これらを連立させることで求まる係数の値から、k1, k-1, k2の値が一意に定まるか否かを判定すれば良い。実際、(4) の係数部分に着目すると、(1) にxEの理想的なデータが与えられた場合、モデルが基本的には同定可能であり、パラメータが一意に定まることが分かる。
ここまで、代数に基づく可同定性解析とその手順を概説した。手順におけるポイントは、その前半部分、つまり、元のモデルにおいて未観測変数xS, xCを消去することで可同定性が判定できる微分方程式を導出するという点である。実際、(1) を眺めていても、パラメータの可同定性に関する情報は得られない。しかし、代数的手法の導入により、(1) から未観測変数を消去すれば、可同定性の問題は、係数に関する連立方程式の解の一意性の問題として捉えられる。このように、変数消去により、解くべき問題をシステマティックに書き換えられる点が、代数的手法のメリットの一つである。
実は、微分方程式で記述されたモデルにおける変数消去は、可同定性解析だけでなく、パラメータ推定にも応用可能である。特に、上記のような変数消去を応用することで、パラメータ間の依存関係なども考慮した推定手法が構築可能である。実際、筆者らは、パラメータ間に隠れた依存関係がある場合、すなわち、同定不可能な場合に有効なパラメータ推定手法を構築した。この手法のメリットは、同定不可能なモデルに対しても、データに適合するパラメータを見落とさない点である15)。また、広い意味での生物学的現象への応用として、筆者らは、タコのような生物の動きを模したロボットであるソフトロボットの代数に基づく解析手法16)も構築しており、従来の解析手法と比べて、実用性の高いアプローチとなっている。このように、多項式微分方程式における変数消去の導入により、生物学に関する現象のモデリングへの新たなアプローチを与えることができる。
5.おわりに
本論文では、変数消去を切り口に、代数生物学の研究例をいくつか紹介した。具体的には、グレブナー基底を用いた変数消去と、モデルリダクションやパラメータ推定問題などへの応用について述べた。本稿では、基礎から応用までの流れを簡潔に述べることを重視し、代数生物学の一部を切り取って説明を行った。しかし、本来、代数生物学ではより多様な代数の理論・技術が、より広範な現象・モデリングへ応用されており、今後も発展の余地がある7)。本稿を一つのきっかけとして、代数生物学への関心が高まれば幸いである。
謝辞
本稿で紹介した研究成果の一部はJST CREST (JPMJCR1914) 及びJSPS科研費JP20J21185の支援のもと得られたものである。
文献
1) Craciun, G., Feinberg, M.: SIAM J. Appl. Math., 65, 1526 (2005).
2) Gross, E., Harrington, H. A., Rosen, Z., Sturmfels, B.: Bull. Math. Biol., 78, 21 (2016).
3) Meshkat, N., Rosen, Z., Sullivant, S.: J. Math. Soc. Japan, In The 50th Anniversary of Gröbner Bases (2018).
4) Macauley, M., Robeva, R.: Lett. Biomath., 7, 81 (2020).
5) Pachter, L., Sturmfels, B.: Algebraic Statistics for Computational Biology (2005).
6) Nardini, J. T., Stolz, B. J., Flores, K. B., Harrington, H. A., Byrne, H. M.: PLoS Comput. Biol., 17, e1009094. (2021).
7) Macauley, M., Youngs, N.: Bull. Math. Biol., 82, 115 (2020).
8) Marsh, L., Dufresne, E., Byrne, H. M., Harrington, H. A.: arXiv, http://arxiv.org/abs/2112.00688 (2021).
9) Cox, D. A., Little, J., O'Shea, D.: Ideals, Varieties, and Algorithms: An Introduction to Computational Algebraic Geometry and Commutative Algebra (2015).
10) Greuel, G.-M., Pfister, G.: A Singular Introduction to Commutative Algebra (2008).
11) Aoki, Y., Hayami, K., Sterck, H. D., Konagaya, A.: SIAM Journal of Sci. Comput., 36, B14 (2014).
12) Miao, H., Xia, X., Perelson, A. S., Wu, H.: SIAM Rev. Soc. Ind. Appl. Math., 53, 3 (2011).
13) Ritt, J. F.: AMS Colloquium Publications, 33 (1950).
14) Forsman, K.: Constructive Commutative Algebra in Nonlinear Control Theory, PhD thesis at Linköping University (1991).
15) 小松瑞果: 時系列データのモデリングにおける代数 的新手法とその展開, 神戸大学 博士論文 (2022).
16) Komatsu, M., Yaguchi, T., Nakajima, K.: Int. J. Robot. Res., 40, 99 (2021).